the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The curious case of the Milankovitch calendar
The Gregorian calendar, despite being more precise than the Julian (which now lags 13 d behind Earth), will also lag a day behind nature in this millennium. In 1923, Milutin Milankovitch presented a calendar of outstanding scientific importance and unprecedented astronomical accuracy, which was accepted at the Ecumenical Congress of Eastern Orthodox churches. However, its adoption is still partial in churches and nonexistent in civil states, despite nearly a century without a better proposition of calendar reform in terms of both precision and ease of transition, which are important for acceptance. This article reviews the development of calendars throughout history and presents the case of Milankovitch's, explaining its aims and methodology and why it is sometimes mistakenly identified with the Gregorian because of their long consonance. Religious aspects are briefly covered, explaining the potential of this calendar to unite secular and religious purposes through improving accuracy in both contexts.
Milutin Milanković (1879–1958; see Fig. 1), or Milankovitch as he is widely known through his works, was a brilliant scientist. He was the first to explain the Earth's cyclical long-term climate changes in terms of three orbital motions whose combined variable effects cause the advance and retreat of polar ice caps, affecting how and when Earth enters an ice age or undergoes global warming based on the insolation (intensity of incoming solar radiation it receives). Accordingly, global climate changes are the result of these cyclical changes in Earth's axis direction, tilt, and the shape of its orbit.
This theory and orbital motions are now known as Milankovitch cycles. It took the world more than 50 years to accept all of it. The main pillar of this theory is the famous Canon of Insolation and the Ice-Age Problem (Milankovitch, 1969), which includes his other results from as early as 1912, including many papers never translated into English – originally in Serbo-Croatian, German, or French (e.g., Milankovitch, 1912, 1913a, b, c, 1920). The theory was finally proven by fossil evidence from ocean cores, as described in a study published in Science, whose authors concluded that “The observed regularity is too great to be explained as a random result” (Hays et al., 1976). This study arose from the global scientific project called “Climate: Long range Investigation, Mapping, and Prediction” (CLIMAP, 1981), which aimed to reconstruct the worldwide climate history through research of deep-sea sediments. After these results were presented, the US National Academy of Sciences officially embraced the Milankovitch cycle model, with the conclusion that “orbital variations remain the most thoroughly examined mechanism of climatic change” (National Research Council, 1982, p. 7). The reliability of the presented isotope data is possibly best judged by the fact that sediment cores from the Atlantic can be correlated with the cores from the Pacific with accuracy completely unknown in any other field of stratigraphy (Schwarzacher, 1993). The variations in the isotopic composition of oxygen in the sediments at the bottom of the ocean follow Milankovitch theory (Rial, 1999), and the changes in the Earth's orbital geometry (characteristics of its orbit and the tilt of its axis) are the fundamental cause of the succession of Quaternary ice ages (Hays et al., 1976). This also concurs with Milankovitch's opinion that the key to past climate change was the way in which the solar radiation reaching the Earth had varied with time and latitude, affecting the amount of ice on the Earth.
The Canon of the Earth's insolation and its application to the ice age problem, initially published in German (Milankovitch, 1941), is his unique masterpiece, which keeps being cited at a constant or even increasing rate (Dimitrijevic, 2002). Therein he collected the results of his 28 research publications and assembled them into one monograph with some new analyses and supplements, and he gave the basis for calculation of climates for all the planets of the Solar System; he himself calculated that daily temperatures on the Moon exceed 100 ∘C (the boiling point of water at 1 atm or 101.325 kPa pressure) and that Mars temperatures are too low for liquid water or any sentient life to exist. This “cosmography” was, in his own words, one of his first and main motives for working out his theory – he said so in the first of his popular books on the history of science, which includes much autobiographical detail (Milankovitch, 1928).
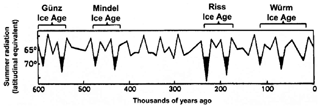
Another great achievement of Milankovitch is tied to the work of another scientist, Alfred Wegener (1880–1930), who proposed continental drift (Wegener, 1912a, b), the forerunner to the theory of plate tectonics, the basis of modern geology. Wegener showed how all continents could fit together as a single continent he called Pangea. He hypothesized that continents drift, and they began to separate about 200 million years ago; this is indeed believed today (e.g., Condie, 1989), proven by the evidence from the ocean floor exploration and also by seismologic evidence (Isacks et al., 1968). It is explained as a consequence of Earth's layered structure and moving plates positioned underneath the continents and oceans. Before all of this was known, about a century ago, Vladimir Köppen, Wegener's father-in-law and his closest associate, sent a letter to Milankovitch saying how excited they both were about the mechanism of cycles he proposed. Their scientific correspondence culminated in 1924 after they jointly published the now classic curve of insolation in Köppen and Wegener's book (1924); this graph of variation in summer radiation for 65∘ N identified the correlation with ice ages (Fig. 2).
Milankovitch was not only among the first ones to accept continental drift theory, but also one of the few who remained loyal to it at the time; after Wegener's untimely death he calculated the secular motion of Earth's rotational poles throughout the history (Milankovitch, 1933), suggesting where they once were and where they are heading. This work, where he mathematically followed the poles' historical trajectories and explained the drift of the Earth's solid crust over its fluid substratum, he dedicated to the memory of Alfred Wegener.
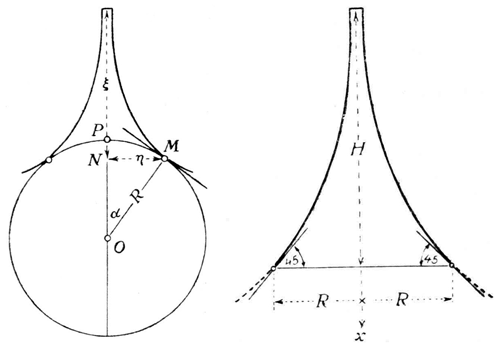
Three years before his death, Milankovitch (1955) calculated the highest building possible on our planet. This “absolute building” would have to be similar to the Eiffel Tower, rotationally symmetrical with a base radius of nearly 113 km, to rise to 20.25 km above the Earth at the highest point P (Fig. 3, left drawing). The point M is where the very shape of our Earth limits further expansion of the base. A smaller rational limit (the right drawing) is simply where the base angle reaches 45∘, because if we want to go higher, from there we are building more in width than in height. Therefore, the rational “modern Babylon Tower” would have a reasonable 2 km base for the height of 13.58 km. Milankovitch specified concrete as the material in his calculations because of its hardening with age, while iron begins to rust; the highest building should thus be made of concrete, reinforced at the higher levels because of the pressure of the wind.
Like closing the cycle, this was not Milankovitch's first trip into Gargantuan endeavors: in his early 1908 article, he described a 1-million-liter water tower and mathematically found its ideal shape that would equalize pressure – the shape of a water drop hanging on a horizontal surface. Hence, his engineering spirit shined ever since he became the first PhD of Technical Sciences from Serbia (his older contemporary Nikola Tesla holds the first honorary degree, while M. I. Pupin, also famous for his electrical engineering contributions, in 1889 obtained his PhD in physical chemistry). His published thesis allowed assessment of the pressure curve's shape and properties when continuous pressure is applied, useful in building of bridges, cupolas, and abutments (Milankovitch, 1907). Before devoting himself to science as professor of celestial mechanics and theoretical physics, he became a much respected civil engineer with six significant patents relating to methods of building with reinforced concrete; his solutions were implemented on dozens of buildings, bridges, and hydro power plants in Europe. How good he was in this work is perhaps best illustrated by the decision of his professors to apply Milankovitch's system in the reconstruction of one of the wings of the Vienna Technical High School itself (Knežević, 2010). He also wrote a number of popular books on the history of science (e.g., Milankovitch, 1928, 1950).
In The Science Book featuring “250 milestones in the history of science” (Singh and Greenfield, 2003), Milutin Milankovitch is listed among the important scientists that shaped our civilization. At NASA, in their edition of the article “On the Shoulders of Giants” (Graham, 2004), Milankovitch was recognized as one of the world's greatest minds of all time in the field of Earth sciences. Since 1993, the Milutin Milankovic Medal has been awarded yearly by the European Geophysical Society (called the European Geosciences Union since 2003), reserved for outstanding contributions in the area of long-term climatic changes and modeling.1 To honor his achievements in astronomy, his name is given to craters on the Moon and Mars and to a planetoid in the main asteroid belt. A good elementary source for more knowledge on his life and theories is The Encyclopedia of Earth biography,2, but it is always worth remembering that Milankovitch was one of the scientists who triggered the transformation of Earth sciences from descriptive into exact.
However, one of his greatest achievements, the most precise calendar of our time, is yet to be accepted by the world.
To better understand the rest of this paper, it is appropriate to review briefly the history of the calendar, with some lesser known facts taken and translated from Milankovitch (1928). Ginzel's three-volume Handbuch, though it dates back more than a century (1906–1914), remains mostly a valuable reference considering calendars and ancient time chronology and can be consulted for more extensive information. Although abbreviations CE (common era) and BCE (before the common era) are more appropriate in interfaith dialogue and science and should be used in accordance with the journal guidelines, the more traditional AD and BC will be used here instead, because the calendar adoption subject has some profound religious aspects, and this article touches upon some of them.
Ancient Egyptians used the year of constant length of 365 d. Thousands of years of experience has shown that this calendar was not in line with nature. The flooding of the Nile was taking place later year after year, just to return to its initial place in the calendar after 1460 years – this was the so-called “Sothic period” or “Sothic cycle”, during which the Egyptian calendar would fall behind nature for the full year of 365 d. From this (dividing 365∕1460), the yearly lag of their calendar was one-fourth of the day. The Ptolemaic calendar reform was proposed and accepted, though never implemented, by the conclave of the Egyptian priesthood in the Decree of Canopus in 238 BC, aiming to keep the calendar synchronized with the seasons. The traditional Egyptian calendar had 12 months of 30 days each and 5 epagomenal days that are outside any regular month. According to the reform, the “Opening of the Year” ceremonies would include an additional sixth day every fourth year, dedicated to the Benefactor Gods, so a sixth epagomenal day would be intercalated every four years in a year of 366 d.
The Julian calendar, still used by the many Orthodox churches today, is the first that actually implemented a 365.25 () days-per-year reform, identical to the Decree of Canopus, in 45 BC in Rome, after the very long realigning “last year of confusion” (Lamont, 1919). In this calendar, leap years occur every fourth year, provided the numerals of that year are divisible by four. Named after and introduced by Julius Caesar, it was made by the astronomer Sosigenes of Alexandria. The seventh month of the calendar got the name Julius, to honor Caesar. At the First Council of Nicea (AD 325), nearly four centuries later, the Christian Church adopted the Julian calendar. Although it has a very good approximation of natural cycles, its year was over 11 min longer than it should be. By the 16th century, the accumulated time difference put the calendar 10 d behind nature, and today it is 13 d behind.
The common calendar of our time, widely used throughout the world, is known as the Gregorian calendar. It is a refinement of the Julian calendar, introduced by the Pope Gregory XIII in AD 1582 and projected by Aloysius Lilius (also variously referred to as Luigi Lilio, Luigi Giglio) after more than three centuries of astronomical reflections in church circles concluded by many theologian scholars, thinkers, and philosophers (the likes of Roger Bacon, Robert Grosseteste, etc.). As a pontifical mathematician and a member of the commission for the reform of the calendar, Ignazio Danti also deserves an honorable mention, as well as another mathematician and astronomer, Christopher Clavius, who finished the proposal of the actual Gregorian calendar after the death of Lilius. The length of the year was adjusted from 365.25 to 365.2425 d, which was just a 0.002 percent change, but it also needed centuries to be widely accepted, especially by non-Catholic countries: the last European states adopted this reform in the 20th century, while the British Empire and its colonies, including what is now the United States, adopted it in 1752 (by which time it was necessary to correct it by 11 d). To achieve the necessary adjustment, the Gregorian calendar skipped the accumulated difference of 10 d (or more, depending when the switch to the new calendar occurred: initially, Thursday, 4 October 1582 was followed by Friday, 15 October 1582). It continues to omit three leap days every 400 years, in a way that years divisible by 100 would be leap years only if they were divisible by 400 as well (so, the years 1700, 1800, and 1900 were not leap years, but the year 2000 was). A calendar mean year is d, with the same result also obtainable by summing the fractional parts implied by the described rule: .
That calendar we still use today in everyday life, but it is not yet completely accurate and is still lagging behind nature, but at a slower rate than its predecessor (26 s per year, compared to the 11 min of the Julian calendar). If we do not want the arbitrary forceful skipping of dates in the future (again), the next common calendar for centuries to come should add another slight but also very important refinement that attaches importance to the synchronization between the civil calendar and the seasons. The one such refinement, proposed by Milutin Milankovitch, would adjust the length of the year to 365.2422 d and leave us – quite naturally instead of forcefully – with the precise calendar for much longer than civilization existed thus far.
The tropical or solar year is, generally speaking, the length of time between two vernal equinoxes (observable and recognizable by equal lengths of day and night), or from spring to spring. However, the time interval between two successive spring equinoxes is (a) not constant, (b) not precisely equal to the tropical year because of precession – the vernal equinox gradually regresses along the ecliptic, and (c) successive passages of the equinoxes are not strictly uniform because the orbital motion of the Earth's line of apses relative to the equinox introduces tiny rate differences, depending on the starting location within the orbit. Hence, using different starting points in the circuit for measurements gives different year lengths – a problem that one usually solves by using the average figure (mean value of all measured yearly time intervals).
The main problem of every calendar is to create years of entire days, each with its own date, but at the same time to comply with the tropical year, which does not have a whole number of days. The most common way to reconcile the two is to vary the number of days in the calendar year. And astronomers have progressively refined the definition of the tropical year, currently defining it as the time interval required for the mean tropical longitude of the Sun to increase by 360∘, or to complete one full seasonal circuit (Meeus and Savoie, 1992, p. 42). Historically, the most often used value for the tropical year is 365.24219878… or 365.2422 d, determined by Newcomb's expression for the geometric mean longitude of the Sun, thus defined as the mean tropical year (Newcomb, 1898). Meeus and Savoie (1992, p. 42) provide its value for the year 2000, which is 365.24219 d, or around 365 d, 5 h, 48 min and 46 s; it slowly shortens, at a rate of approximately half a second per century, and it lasted 365.24231 d in the astronomical year 0, coinciding with the Julian year 1 BC. There is a regular expression that gives the length of the tropical year (Y) as a function of the time in Julian centuries (t), based on the tables of Newcomb: . Another slightly different starting value was suggested by Le Verrier, and both equations estimate that the tropical year become over half a second shorter each century, or in case of Milankovitch's calculations (1923) precisely 0.539136 s, though he explicitly states that we can not talk about the mean value for the length of the tropical year in general terms, but only for a certain epoch, as we presently do not know how it will change in the future.
Milankovitch analyzed the Earth's period of rotation, which he believed was not constant, and that a seasonal year was not of a constant length (like many before him suspected: Hipparchus, Copernicus, Kepler) – this was nearly impossible to measure precisely until the first atomic clock, based on a transition in the cesium atom, was made in 1955 by Essen and Parry. The General Conference on Weights and Measures in 1960 even redefined the measure of second in terms of this cesium transition. The atomic second, often called the SI second, was meant to agree with the ephemeris second based on Newcomb's work, which also makes it agree with the mean solar second of the 19th century (for more details, see McCarthy and Seidelmann, 2009). The discovery that the rate of rotation of the Earth, and in turn the length of mean solar day, is not constant was important in understanding the tropical year changes over long periods of time. And Milankovitch proposed an elegant technical solution, both simple and effective, that put into perspective his (at the time) suspicions about the length of the tropical year in the long run and gave us the calendar of the unprecedented accuracy – more accurate than the Gregorian calendar and still so attuned to it that the first deviation between the two would occur in the year 2800.
The calendar was proposed by Milutin Milankovitch at the Ecumenical Congress of Eastern Orthodox churches in Constantinople (shortly before it became Istanbul) in May 1923. Milankovitch was invited by his government to be its representative at the summit because it was recognized that “astronomical sciences have a final say on calendar issue”, and he was the leading expert at the time; the Serbian Orthodox Church accepted the government's choice (Milankovitch, 1928). The main topic of discussion at this gathering was the reform of the Julian calendar, which was already 13 d behind the Gregorian calendar used in the West. The main purpose of the reform was to unify the days when the saints are celebrated in both Christian churches (Orthodox and Catholic) and avoid double celebrations that introduce confusion and financial losses for national economies. Milankovitch was the second member of Serbian royal delegation and, in his own words, “the only civilian at the congress, because the two professors of theology count, despite their civil uniforms, in the priestly caste” (Milankovitch, 1928). At the time, it had been more than a decade since Milankovitch gave up his successful civil engineering career in Vienna to accept, for a salary 10 times lower, the call from the famous Serbian professor-scientists Jovan Cvijić, Mihailo Petrović Alas and Bogdan Gavrilović and take position of Chair of Applied Mathematics at the University in Belgrade, Kingdom of Serbia. The position included three seemingly diverse subjects that, as Milankovitch later believed, helped his scientific development: rational mechanics, celestial mechanics, and theoretical physics. Shortly afterwards, he spent World War I as a detainee in Budapest after being arrested on his honeymoon – it was during the war years that he really developed his astronomical and mathematical theory of climate, before publishing his important results in a French-language monograph (Milankovitch, 1920).
The Serbian delegation came to the 1923 congress with a proposition for calendar reform by another author, Maksim Trpković, which was later rejected, but it is important to mention it because Milankovitch initially took over the calculations for the date of Easter from there. The Greek delegates, however, improved the final proposition by suggesting that the date of Easter should be determined by astronomical observations; Milankovitch agreed wholeheartedly, as this was the scientific way. Trpković originally proposed the intercalation rule that the secular or centennial years (ending with two zeros and thus divisible by 100) in centuries which when divided by 9 have remainders of 0 or 4 will be leap years. In such a way 7 days will be skipped in nine centuries, so that the calendar will be closer to the tropical year than the Gregorian calendar, and the vernal equinox will always fall close to 21 March. A scientific commission was formed to examine the two proposals (the second was Romanian, which suggested too many changes to be acceptable), but both were rejected by the congress. What they found objectionable in the proposition of the Serbian delegation was the fact that the year 2000 would not be a leap year, as opposed to the Gregorian calendar, and after only 77 years a difference of 1 d would appear between the Gregorian calendar and the newly rectified one. The general opinion of the participants was that the better solution was to retain the Julian calendar as it was, and only delete 13 d in order to bring it in line with the Gregorian calendar because compliance of dates was considered mandatory. In this way, the first 1-day difference would appear 100 years later. Another option was to completely adopt the Gregorian calendar (Milankovitch, 1924).
At the congress (but also in the scientific monograph that followed – see Fig. 4), Milankovitch (1923) scientifically presented that the Gregorian calendar, despite being more precise than the Julian calendar, is also not precise enough and that it will be a whole day late in our present millennium. This fact was, and still is, the call for the new reform of both Julian and Gregorian calendars.
Milankovitch was then asked to try to revise the calendar during the congress (which lasted nearly a month), to make it more astronomically consistent and acceptable for all. His well-documented proposal was accepted at the congress but, for various bureaucratic reasons, some of which are mentioned in this article, the implementation is still lagging behind even in the Orthodox churches.
As a starting point, he tried to obtain the longest possible consonance of the two calendars, realizing from the congress discussion that a realistically acceptable proposal must be strictly scientifically based and astronomically more precise than the Gregorian calendar but also very similar to it (Milankovitch, 1923). Days later, he developed a new intercalation rule for leap years, but only after a long night without sleep, during which he felt the need to “drink a lot of coffee and smoke a lot of tobacco like a Turkish pasha” (Milankovitch, 1928 – the style of this popular book shows his literary qualities that bring historical occasions closer to the reader). In addition to the “every fourth year” rule that had been constantly in effect since Julius Caesar, centennial years (always divisible by 100) would be leap years only if division by 900 left a remainder of 200 or 600 (unlike the Gregorian rule, requiring division by 400 without a remainder).
Milankovitch selected this rule because it yields 218 leap years in the 900-year period, so d, producing an average year length that is almost identical to the then current length of the mean tropical year (a 2 s difference if we go further in decimals). Despite slow changing of the year length, he considered this precision sufficient for numerous future millennia. In this way he obtained a calendar that was more precise than the Gregorian but consistent with it up to 2800, which was 877 years from that Ecumenical Congress in Constantinople, or a whole 800 years longer consistency than with the previous Serbian proposition! The results (see Fig. 5) were that the years 2100, 2200, 2300, 2500, 2600, and 2700 are ordinary according to both calendars; the years 2000 and 2400 are leap years according to both calendars, since 2000 and 2400 can be evenly divided by 400. According to the calendar presented by Milankovitch, when 2000 is divided by 900, the remainder is 200 and for 2400 the remainder is 600. The year 2800 is a leap year only according to the Gregorian calendar, since 2800 can be evenly divided by 400, but when divided by 900 the remainder is only 100, which makes it an ordinary year, unlike the year 2900.
Although an academic paper is not expected to deal extensively with religious aspects, a few words should be said about them in view of the importance that religious leaders historically had in the adoption of the calendars. There is no calendar reform that has received widespread reception without the unanimous consent of religious leaders, as described at length by the masterly review published by Grumel in 1958. Proceedings of the Vatican conference to commemorate the 400th anniversary of the “Gregorian Reform of the Calendar” (Coyne et al., 1983) mentions the calendar presented here, which “improves upon the year length of the Gregorian scheme, so that leap years will include 2000, 2400 (as in the Gregorian calendar), but also 2900 and 3300 instead of 2800 and 3200; thus the dominions of the Eastern Orthodox Church will differ by a day from the rest of the world in the 29th century AD”.
When adopting the Julian calendar, the Nicene Council of AD 325 sought to devise rules according to which all Christians would celebrate Easter on the same day, or to quote presumably Eusebius (339, translated in 1999) and his unfinished work: “Think, then, how unseemly it is, that on the same day some should be fasting whilst others are seated at a banquet; and that after Easter, some should be rejoicing at feasts, whilst others are still observing a strict fast.” It took a very long time for Christians to achieve that objective in AD 325. Afterwards, the papal bull Inter gravissimas, issued by Pope Gregory XIII on 24 February 1582, became the law of the Catholic Church, but it was never recognized by any of the Orthodox churches or by Protestant churches, among others. Consequently, the days on which Easter and related holidays were celebrated by different Christian churches diverged once again.
What is called the Milankovitch calendar in this article is actually the result of the cooperation of numerous churches, spiritually in line with the original meaning of the word “synod”. The Serbian delegation gave up on its denied proposition, and Milutin Milankovitch later proposed the improved calendar described here. The Greek delegation proposed that the phases of the moon and the date of Easter should not be calculated from the 19-year Metonic cycle of golden numbers and epacts (add 1 to the year and divide by 19, the reminder is the “golden number”…), because that system of numbers corresponding to the different lengths of the solar and lunar years is not equal for the Julian and Gregorian calendar, and the results of both computations are incorrect (Milankovitch, 1928); instead, the date of Easter should be determined in the future by precise astronomical calculations and through cooperation of astronomical observatories and departments of celestial mechanics at the universities of Athens, Belgrade, Bucharest, and St. Petersburg. This was in accordance with the simple rule accepted by all Christian churches at the First Council of Nicea in AD 325 that Easter should be celebrated on a Sunday, later than the vernal equinox (which was fixed on 21 March), on a date to be decided conjointly by Rome and Alexandria. The first full moon after the vernal equinox is the now accepted rule, but it is only in the 6th century that Easter tables wrongly assigned to Cyril of Alexandria assumed this rule (see Grumel, 1960). It is clear and unequivocal that no difference would be possible in regard to the date of Easter if the phases of the moon are accurately determined, and not by the old rules of reckoning, which gave inaccurate results (Shields, 1924); these inaccuracies are explained in detail by Milankovitch (1923, 1924). The Romanian delegation gave up on its denied proposition and raised the issue of initiative of Orthodox churches to convene a world congress on the calendar issue after the unifying proposition of Milankovitch's calendar. These steps were aimed to bring all Christian calendars in agreement. All delegates present at Ecumenical Congress of 1923 gave their contribution to the shaping of the final proposition.
The Russian Church was the first to accept the revised calendar after the Synod of the Church of Constantinople (Milankovitch, 1923; Shields, 1924) but later indefinitely delayed its implementation, possibly because the Russian representation, in the troubled times of the Bolsheviks, came to the congress not from the Russian Church, but from the newly formed schismatic Renovationist Church (Stamatopoulos, 2008), which soon went into decline and ceased to exist in 1946. The Serbian Church also delayed implementation after its initial acceptance, for the time “when the reformed calendar is accepted and implemented by all the other Orthodox Churches.”
Today, for example, the Patriarchates of Constantinople, Alexandria, and Antioch and churches of Greece, Cyprus, Bulgaria, Romania, Poland, Albania, Czech Republic, and Slovakia up to the Orthodox Church in America (since 1983) use the “new”, “revised” or “rectified” Julian calendar with a different leap-year rule, which dropped 13 d in 1923 and can be easily referred to as the Milankovitch calendar, by the name of the author of the main corrections, until the time it eventually became known by the name of the religious authority that instills the unity of calendar acceptance to all. Until 2800, churches mentioned so far in this paragraph will celebrate Christmas on the same day as the Western churches; after that, they will celebrate on the astronomically more precise date, unless all the churches accept the Milankovitch calendar by then. Of those which continue to adhere to the old Julian calendar, at the present time, there is the Patriarchate of Jerusalem and the churches of Russia and Serbia, along with the monasteries on autonomous monastic state of Mt. Athos. They will continue to celebrate Christmas on 25 December in the Julian calendar, which is 7 January in the Gregorian calendar until 2100, when it will become 8 January. The Oriental Orthodox churches (Coptic, Ethiopian, Eritrean, Syrian and the Armenian Apostolic Church) will continue to use their own calendars, which usually result in fixed dates being celebrated in accordance with the Julian calendar, except (for part of) the Assyrian Church.
All Orthodox churches still continue to use the Julian Easter, with the sole exception of the Finnish Orthodox Church, so determining the date of Easter by precise astronomical calculations is not yet widely accepted, although it is accepted that the date of Easter should always be determined by the time of the holy city of Jerusalem. A precise astronomical rule for Pascha (Easter, Pasch), determined by general Synod in 1923, states the following: Pascha is the Sunday after the midnight-to-midnight day at the meridian of the Church of the Holy Sepulchre in Jerusalem during which the first full moon after the vernal equinox occurs; the instant of the full moon must occur after the instant of the vernal equinox, but it may occur on the same day; if the full moon occurs on a Sunday, Easter is the following Sunday.
Our calendars have become more precise throughout history, thus improving the emulation of the natural cycle that does not have a whole number of days measured by our seconds. Milankovitch achieved accuracy of 365 d, 5 h, 48 min and 48 s. His calendar year is only two and a fraction seconds longer than the current tropical year. If we compare it with historically popular calendars, the results are impressive: the Julian calendar loses a whole day in the race with nature every 128 years, and the Gregorian calendar is only somewhat more durable with its 3280 years before trailing behind a full day. Of course, nature always wins, but the Milankovitch calendar is a clear runner-up, with the full 28 800 years of running in parallel with nature. Perhaps we should give the future generations the solution to the measurement of time, the one that will not eventually leave them in the past.
Although attuned for the longest possible consonance, the Gregorian and Milankovitch calendars will finally show a serious disagreement in the year 2800, when 1 March 2800 in the Milankovitch calendar will be 29 February 2800 in the Gregorian calendar. So that year will be a leap year only according to the less precise Gregorian calendar, which will be a whole day late even during our millennium, and at least full 3 d (Blackburn and Holford-Strevens, 2003), or more likely 10 (Borkowski, 1991), behind the natural seasons after about 10 millennia. The year 2800 is the last reasonable date to accept the Milankovitch calendar, with many advantages explained in this study, although it would be more sensible for the world to do it much earlier (we are closing to the centennial of its “birth”, which is the year 2023). It is important to emphasize that, for the majority of civil purposes, there will be no visible difference from the currently used calendar until the year 2800; that is actually one of the strongest points for its acceptance, as the higher accuracy would be achieved without compromising the old habits for quite a few centuries.
If society in the future still attaches importance to the synchronization between the civil calendar and the seasons, the reform of the calendar will be necessary. Borkowski (1991, p. 121) states that due to “high uncertainty in the Earth rotation it is premature at present to suggest any reform that would reach further than a few thousand years into the future.” Proposal of calendar reform suggested by Milankovitch is nearly a hundred years old and is becoming very relevant in this millennium.
This paper has hopefully shed some light on the least recognized contributions of one of the greatest geoscience and space sciences minds of all time; it perhaps to a small extent contributes to the adoption, both for secular and for religious purposes, of his calendar, which is more accurate in keeping up with nature than the other ones. The process of adopting a calendar usually lasts centuries, so it can be assumed that the Milankovitch calendar began its journey long ago, and this paper needed only to focus attention to the problem and its solution: a scientifically relevant and astronomically precise unifying calendar that is suitable for all and for many centuries to come.
The author declares that there is no conflict of interest.
Thanks are owed to referees and the editor, Pascal Richet, for their suggestions and additional literature that improved this work. All potential mistakes remain mine.
This paper was edited by Pascal Richet and reviewed by two anonymous referees.
Blackburn, B. and Holford-Strevens, L.: The Oxford Companion to the Year, Oxford University Press, corrected reprint of 1999, 2003.
Borkowski, K. M.: The tropical year and the solar calendar, J. Roy. Astron. Soc. Can., 85, 121–130, 1991.
CLIMAP: Seasonal reconstructions of the Earth's surface at the last glacial maximum in Map Series, Technical Report MC-36, Geological Society of America, Boulder, Colorado, 1981.
Condie, C. K.: Plate Tectonics and Crustal Evolution, 3rd ed., Pergamon Press, 1989.
Coyne, G. V., Hoskin, M. A., and Pedersen, O. (Eds.): Gregorian Reform of the Calendar: Proceedings of the Vatican Conference to Commemorate its 400th Anniversary (1582–1982), Rome, 1983.
Dimitrijevic, M. S.: Milutin Milankovtch (1879–1958) and his contribution to European astronomy, Astron. Nachr., 323, 570–573, 2002.
Eusebius, C. P.: On the Keeping of Easter, in Vita Constantini, Lib. iii., translated into English by: Averil, C. and Hall, S. G., translated reprint of 339, Clarendon Press, Oxford, 18–20, 1999.
Ginzel, F. K.: Handbuch der mathematischen und technischen Chronologie, Bd 1–3, Hinrichs, Leipzig, 1906, 1911, 1914.
Graham, S.: Milutin Milankovitch, NASA On the Shoulders of Giants, available at: https://earthobservatory.nasa.gov/features/Milankovitch (last access: 14 May 2017), 2004.
Grumel, V.: Traité d'études byzantines, I, La Chronologie, PUF Bibliothèque Byzantine, Paris, 1958.
Grumel, V: Le problème de la date pascale aux IIIe et IVe siècles, Revue des Études Byzantines, 18, 163–178, 1960.
Hays, J. D., Imbrie, J., and Shackleton, N. J.: Variations in the Earth's Orbit: Pacemaker of the Ice Ages, Science, 194, 1121–1132, 1976.
Isacks, B., Oliver, J., and Sykes, L. R.: Seismology and the New Global Tectonics, J. Geophys. Res., 73, 5855–5899, 1968.
Knežević, Z.: Milutin Milanković and the astronomical theory of climate changes, Europhysics News, 41, 17–20, 2010.
Koppen, V. and Wegener, A.: Die Klimate der geologischen Vorzeit [Eng: Climates of geological Past], Gebrüder Borntraeger, Berlin, 1924.
Lamont, R.: The Roman calendar and its reformation by Julius Caesar, Popular Astronomy, 27, 583–595, 1919.
McCarthy, D. D. and Seidelmann, P. K.: TIME: From Earth Rotation to Atomic Physics, Wiley–VCH Verlag GmbH and Co, Weinheim, 2009.
Meeus, J. and Savoie, D.: The history of the tropical year, Journal of the British Astronomical Association, 102, 40–42, 1992.
Milankovitch, M.: Theorie der Druckkurven, Zeitschrift f. Mathematik und Physik, 55, 1–27, 1907.
Milankovitch, M.: O membranama jednakog otpora [Eng: On membranes with equal resistance], Rad Jugoslavenske Akademije Znanosti i Umetnosti, M-P r 125, (44), 140, 1908.
Milankovitch, M.: Prilog teoriji matematske klime [Eng: On the mathematical theory of climate], Glas Srpske Kraljevske Akademije, 87, 136–160, 1912.
Milankovitch, M.: O rasporedu sunčeve radijacije na površini zemlje, Glas Srpske Kraljevske Akademije, 91, 101–179, 1913a.
Milankovitch, M.: O primjeni matematičke teorije sprovođenja toplote na probleme kosmičke fizike, Rad Jugoslavenske Akademije Znanosti i Umetnosti, M-P r 200, 109–121, 1913b.
Milankovitch, M.: Uber ein Problem der Warmeleitung und dessen Anwendung auf die Theorie des solaren Klimas, Zeitschrift f. Mathematik und Physik, 62, 63–77, 1913c.
Milankovitch, M.: Theorie Mathematique des Phenomenes Thermiques produits par la Radiation Solaire [Eng: Mathematical Theory of Heat Phenomenon Produced by Solar Radiation], Gauthier-Villars, Paris, 1920.
Milankovitch, M.: Reforma Julijanskog kalendara [Eng: The Reform of the Julian Calendar], Srpska Kraljevska Akademija nauka i umetnosti, Belgrade, 1923.
Milankovitch, M.: Das Ende des julianischen Kalenders und der neue Kalender der orientalischen Kirchen, Astron. Nachr., 220, 379–384, 1924.
Milankovitch, M.: Kroz vasionu i vekove: pisma jednog astronoma [eng. Through Distant Worlds and Times: Letters from a Wayfarer in the Universe], Matica srpska, Belgrade, 1928.
Milankovitch, M.: Sakulare Polverlagerungen [Eng: Secular shift of the Poles], in: Handbuch der Geophysik, edited by: Gutenberg, B., Bd 1 L 2 Ab VII, Gebrüder Borntraeger, Berlin, 1933.
Milankovitch, M.: Kanon der Erdbestrahlung und seine Anwendung auf das Eiszeitenproblem, Srpska kraljevska akademija, Belgrade, 1941.
Milankovitch, M.: Kroz carstvo nauka [Eng: Through the Empire of Science], Naučna knjiga, Belgrade, 1950.
Milankovitch, M.: Babylonian Tower of modern techniques, Glas CCXX Section of Technical Sciences of the Serbian academy of Sciences, 3, 137–50, 1955.
Milankovitch, M.: Canon of Insolation and the Ice–Age Problem, translated reprint of 1941, Israel Program for Scientific Translations, Jerusalem, 1969.
National Research Council: Solar Variability, Weather, and Climate, National Academy Press, Washington, DC, 1982.
Newcomb, S.: Tables of the four inner planets (Vol. 6), in: Astronomical papers prepared for the use of the American ephemeris and nautical almanac, 2nd Edn., Bureau of Equipment, Navy Dept, Washington, 1898.
Rial, J. A.: Pacemaking the ice ages by frequency modulation of Earth's orbital eccentricity, Science, 285, 564–570, 1999.
Schwarzacher, W.: Cyclostratigraphy and the Milankovitch theory, Developments in Sedimentology, 52, 1–225, 1993.
Shields, M. N.: The new calendar of the Eastern churches, Pop. Astronomy, 32, 407–411, 1924.
Singh, S. and Greenfield, S. (Eds.): The Science Book, Weidenfeld and Nicolson, London, 2003.
Stamatopoulos, D.: A Quest for Reform of the Orthodox Church: The 1923 Pan-Orthodox Congress: An Analysis and Translation of its Acts and Decisions review, J. Mod. Greek Stud., 26, 518–521, 2008.
Wegener, A.: Die Herausbildung der Grossformen der Erdrinde (Kontinente und Ozeane) auf geophysikalischer Grundlage, Petermann. Geogr. Mitt., 63, 185–195, 253–256, 305–309, 1912a.
Wegener, A.: Die Entstehung der Kontinente, Geol. Rundsch., 3, 276–292, 1912b.
European Geosciences Union: Milutin Milankovic Medal, available at: https://www.egu.eu/awards-medals/milutin-milankovic/, last access: 30 March 2019.
Lee, J.: Milankovitch Milutin, available at: http://www.eoearth.org/view/article/154611 (last access: 12 March 2015), 2012.